Proč je rychlost světla stále neměnná - relativita snadno a názorně...
Dnes si vysvětlíme podstatu speciální teorie relativity, stálou rychlost světla, tento její základní axiom. (Upozorňujeme ale, že výklad bude pouze názorně metaforický, ostatně tohle je blog, ne fyzikálně plně korektní.)
Speciální teorie relativity je "zjednodušená" teorie relativity, která platí jen pro systémy, na které nepůsobí žádné zrychlení. Výkladem stálé rychlosti světla je vyloženo vlastně to hlavní ze speciální teorie relativity. Není to ale až tak názorné, protože výklad bude ke konci čtyřrozměrný, ale my žijeme v trojrozměrném prostoru. Proto v příštím blogu vyložíme velmi prostě dilataci (zpomalení) času, což bude názorný výklad toho, jak relativita funguje v našem 3D prostoru. Pak bude všem tato teorie jasná. :-)
Vysvětleme si tedy, jak je to s tou rychlostí světla. Představme si, že jsme ve člunu na klidném jezeře a onen člun je také v klidu. Když hodíme do vody vedle lodi kámen nebo zahýbeme celou lodí, vytvoříme vlny, které se šíří na všechny strany stejnou rychlostí a proto vytvářejí kruhy. Že je loď v klidu, to právě poznáme podle toho, že zůstává stále ve středu těchto soustředných kruhů, které jsme předtím např. lodí vyvolali (viz obrázek 1).
Jakmile se ale potom, co vlny vytvoříme, začneme s lodí pohybovat na nějakou stranu, opustíme tím nutně střed kruhů. Skončíme třeba v červeném bodě vpravo, viz druhý obrázek. Jestliže ale zpozorujeme, že loďka zůstala na konec ve středu kruhů, máme jistotu, že jsme se vůči vodě nehýbali, byli jsme vůči ní stále v klidu. Je to prosté: jestliže jsme zůstali stále ve středu, byli jsme v klidu, jestliže jsme mimo střed, pohybovali jsme se.
Udělejme to tak, že ve chvíli, kdy hodíme například cihlu do vody, a ta vytvoří vlny, budeme mít ve středu loďky dvě (a cihlu hodíme třeba mezi ně). Loďka 1 zůstane v klidu ve středu kruhů. Loďka 2 se v okamžiku dopadu cihly začne pohybovat nějakou stálou rychlostí a skončí za nějakou dobu v červeném bodě, viz obrázek 3.
Pochopitelně je zcela nemyslitelné, aby obě loďky, které se vůči sobě pohybují, zůstaly ve středu těchto kruhů vln. Jenže právě to se naměřilo v případě světelných vln ! Když se zjistilo, že je světlo elektromagnetické vlnění, automaticky se předpokládalo, že se vlní nějaké médium (jako je třeba vzduch nebo voda) a toto médium bylo nazváno éter. A tento hypotetický éter se choval právě takto podivně, že ať se v něm těleso pohybovalo jakoukoliv rychlostí, zůstávalo vždy ve středu vln, které před nějakým časem vyvolalo.
Jestliže ale každé těleso vždy zůstane ve středu kruhových vln (v případě prostoru jsou to vlny kulové), je zcela jasné, že tyto vlny mají vůči každému tělesu na libovolnou stranu stejnou rychlost a to i u dvou těles, která se třeba od sebe vzdalují nebo se k sobě přibližují. Právě proto má světlo neustále stejnou rychlost c (cca 300 000 km/s) vůči každému tělesu, každému pozorovateli, vůči každé "loďce" pohybující se libovolnou rychlostí a vůči každému pozorovateli v této "loďce". Zkusíme-li se vydat za světlem velkou rychlostí, jeho rychlost nezmenšíme, stejně jako ji nezvětšíme tím, že mu poletíme obrovskou rychlostí vstříc.
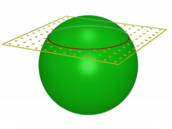
Ale jak je něco takového možné, když to vlastně možné není???!!!! Řešení je poměrně prosté. Elektromagnetické vlnění je totiž (nejméně) čtyřrozměrné, protože se děje v tzv. 4D časoprostoru. To se zobrazuje dosti těžko, takže pro názornost ubereme jeden rozměr. Místo 4D vlnění budeme popisovat 3D vlnění, tedy jakousi kouli vlnění, kterou vidíme na následujícím obrázku 4.
Dobře si představíme, že 3D vlnění je vlastně soubor takovýchto koulí se stejným středem. A tyto koule se rozpínají, podobně jako se rozbíhají kruhy na vodě. A kde je náš prostor? To je dvojrozměrná rovina, která tyto koule řízne. Ostatně dva taková řezy (i když jen polořezy) na obrázku 4 už jsou. A v každém krásně vidíme stejné kruhy, jako jsme viděli na vodě.
Jenže, je-li náš prostor nějaký takový 2D řez, který ufikne "špičku" té koule (viz obrázek 5), pak dostaneme kruhy stejné jako na vodě. Takový řez vidíme například na obrázku 6. Jenže pak jsme ale ve stejné situaci jako s loďkami na vodě na obrázku 3. Máme jedny kruhy, v jejichž středu může zůstat jen jedna "loďka", zatímco druhá, která se vůči této klidové "loďce" pohybuje, musí střed kruhů opustit, ne?
Jenže to je právě to kouzlo světla šířícího se vesmírem, že ten řez není jediný. Každé těleso si podle své rychlosti v prostoru vytvoří vlastní řez, každé těleso má vlastní prostor. To jen ten šok, který objevila speciální teorie relativity. Každá (stálá) rychlost v prostoru znamená jen různé vyklonění tohoto řezu. Takže vlastně každé těleso, podle své rychlosti, má svůj vlastní, jinak skloněný prostor.
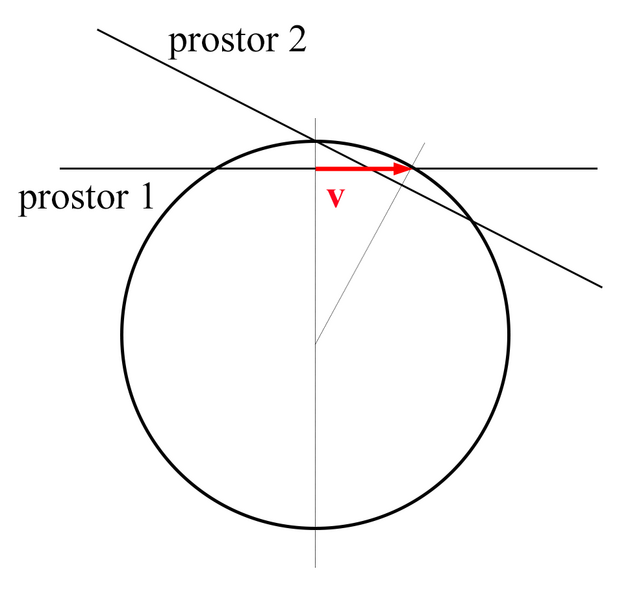
Na posledním obrázku 7 vidíme dva takové vůči sobě skloněné prostory (i když jsme pro jednoduchost ubrali ještě další dimenzi a prostorem je zde přímka, která řeže kruh(y)). Každé těleso má své vlastní vlnové kruhy, v jejichž středu se drží. O míře vyklonění jedněch kruhů vůči druhým, jednoho prostoru vůči druhému, rozhoduje rychlost v mezi tělesy, která je na obrázku znázorněna červeným v. Poloměr kruhu je pak rychlost světla c. Hle, nazřeli jste samotnou podstatu Einsteinovy speciální teorie relativity.
Příště si názorně předvedeme, jak se tento 4D mechanismus projevuje v našem obvyklém trojrozměrném prostoru v podobě dilatace času.
(Poznámka jen pro experty: Vím, že jsem v posledním obrázku pro jednoduchost nakreslil rychlost v opačné orientaci.)
Jan Fikáček
Proč jsou izraelská média daleko méně proizraelská než česká?

A nejde jen o izraelská média. USA jsou přece dlouholetý a věrný spojenec Izraele, ale ani ony nestojí teď vždy na straně Izraele. Proč? Proč se snaží válečné tažení Izraele brzdit a volají po příměří?
Jan Fikáček
Tak přece má foton hmotnost!?

Fyzika je úžasná věda, která proměnila celou naši civilizaci. Stačí vzpomenout třeba jen elektřinu bez níž by nebyly počítače, mobily, TV, osvětlení našich bytů atd. Ovšem výjimečně se v ní objeví i dost iracionální tvrzení.
Jan Fikáček
Solvay institut - Einstein, Schrödinger, Planck, Heisenberg, Bohr atd.

Od roku 1911 se konají Solvayovské konference, kterých se ve dvacátých letech účastnili dnes nejslavnější fyzici jako Einstein, Planck, Bohr, Heisenberg. Tyto konference jsou známé hromadnými fotografiemi nejslavnějších fyziků.
Jan Fikáček
Nahraďte svou ženu a děti umělou trpělivostí (inteligencí?)!

Tak jo, uznávám, že ženu a děti nelze umělou inteligencí nahradit ve většině případů, ale v jednom by to asi šlo, ne? :)
Jan Fikáček
Mašínové: Padouch nebo hrdina, my jsme jedna rodina!

Film Bratři o skupině Mašínů dostal v sobotu cenu za nejlepší film roku na Českém lvu. Jeho tvůrce na večeru prohlásil, že to byli hrdinové. Tak se pojďme podívat na jejich činy.
Jan Fikáček
Jak nás intuice vede na scestí v otázce, co je to realita

V hollywoodských filmech často nějaký hrdina, astronaut nebo detektiv, vyřeší problém intuicí. Když selže rozum a důkazy, intuice zaskočí. Jenže intuice není vždy spásné řešení, někdy tomu řešení naopak brání..
Jan Fikáček
Dá se v padesáti naučit anglicky?

Mnohokrát jsem slyšel názor, že pokud se člověk nenaučí nějaký cizí jazyk do třiceti, už se ho nenaučí nikdy. A proto když jsme se přestěhovali s rodinou před tímto mým věkem do Belgie, ani jsem se nový jazyk naučit nesnažil.
Jan Fikáček
Kdy věčnost trvá jen 40 minut

Nositel Nobelovy ceny za fyziku z roku 2012 Franz Wilczek vymyslel kdysi tak zvané časové krystaly. Teď vědci objevili jejich nový druh, o němž dokonce někdo prohlásil, že je nesmrtelný.
Jan Fikáček
Jak se něco naučit 10x rychleji? Použijte AI !

Znáte ten typ lidí, kteří se do něčeho zakousnou a dělají to 12 hodin denně, ať jsou to motorky, stavba baráku nebo věda. Tak takový já určitě nejsem. Ale i takoví jako já mají šanci stát se v něčem machry a to velmi rychle.
Jan Fikáček
O tom, že bakterie myslí tak jako my

Jestli si myslíte, že si chytnete nějakou bakterii a pokecáte si s ní, tak to těžko. Ona "mluví", pokud víme, jen s viry. Ukážeme si třeba, jak bakterie umí abstraktně zobecňovat! Cože? To přece umíme jen my lidé, ne?
Jan Fikáček
Pochopte kvantovou mechaniku za minutu díky sněhové vločce a umělé inteligenci

Kvantová mechanika je nepochopitelná jen tehdy, když člověk nerozumí jejímu filosofickému základu. I nedávní nositelé Nobelovy ceny za fyziku prohlašují, že kvantová mechanika dokazuje, že realita neexistuje. Jak prostý omyl.
Jan Fikáček
Zvládněte portrét s umělou inteligencí za minutu (1 minuta)

Existuje mnoho dlouhých článků a hodinových videí o AI (Artificial Intelligence), které vás zahltí spoustou nepotřebných informací. Chcete-li ale za minutu něco s AI nakreslit, čtěte tento blog. Povedu vás zkratkou.
Jan Fikáček
O tom, proč jsou Beatles, Galileo či Einstein všudypřítomní jako bůh

Když jsem svému synovi pěl chválu na skupinu Beatles, znechuceně odvětil, že je to hudební pravěk. No jasně, dnes jede něco úplně jiného. Dcera mě třeba uvrtala do K-popu (korejského popu), syn stále poslouchá nějaké Bla, bla...
Jan Fikáček
Má Česko milióny chudých? Nebo je to výmysl podporující Babiše?

Na Novinkách.cz vyšel článek o průzkumu chudoby v Česku. Co mě ale zaujalo snad ještě více bylo, jak ho někteří zastánci současné vlády označili za podporu Babiše a SPD. Mohou být fakta úmyslnou podporou nějaké politické strany?
Jan Fikáček
Hitler přežil mnoho atentátů. To já ale taky!

Je známo, že se Hitler už za první světové války ocitl bezbranný před ozbrojeným nepřátelským vojákem, který ho mohl snadno zastřelit. Ten voják se ale slitoval. Kdyby věděl! Hitler vlastně mnohokrát unikl smrti.
Jan Fikáček
Kde jsou všichni mimozemšťané? Syndrom velkého opuštěného hnízda.

Probudil jsem se do dokumentárního pořadu o dinosaurech, kde se řešilo, že velcí dinosauři nemohli sedět přímo na vejcích, protože by je rozmačkali. Vejce proto byla ve velkém kruhu a dinosaur seděl na volné zemi uprostřed nich.
Jan Fikáček
Kunderův Žert aneb kdy není "fanatismus" úplně blbý

„Milá Markéto, optimismus je opium lidstva. Zdravý duch páchne blbostí. Ať žije Trockij. Tvůj Ludvík" byl Ludvíkův politický žert, který mu zničil život. Podobné zážitky člověk ale mohl mít i později než v 50. letech.
Jan Fikáček
Cikánka: Ty jsi policie? Dáš mi pajsku?

Pocházím z Ostravy, tak mám s romskou komunitou bohaté zkušenosti. Ale některé reakce mě i tak překvapí. Jo, bylo by správnější říkat Romka, ale dotyčná taky poznamenala, že není žádná Romka, ale Cigoška. Tak to respektuju.
Jan Fikáček
Existuje čas? Nebo existuje jen současnost? Váš pohled na Měsíc je důkazem. (1 minuta)

Existuje nápaditá koncepce, která tvrdí, že minulost ani budoucnost neexistují, že existuje jen přítomnost. Že třeba žádní dinosauři neexistovali, že nějaká superinteligence nastražila všechny ty kosti v současném okamžiku.
Jan Fikáček
Mašínové všech zemí, spojte se! (2 minuty)

Mašínové jsou pro některé lidi vrazi, pro některé velcí hrdinové. Tedy přesněji celá jejich skupina čítající původně šest lidí. A jako obvykle si obě strany skoro vždy dělají názor bez základních znalosti o této skupině.
| předchozí | 1 2 3 4 5 6 7 ... | další |
- Počet článků 310
- Celková karma 30,39
- Průměrná čtenost 3149x
Chcete-li sledovat diskuse v "jeho" skupině, připojte se do Vědecké filosofie & Fyziky (nejen). jfikacek@gmail.com
Upozornění: Toto je popularizační blog pro veřejnost, neberte ho tedy jako vědeckou dizertační práci. Někdy je to jen divoká fantazie. Na druhé straně se snaží udržovat jistou vědeckou kvalitu, takže "esoterické" komentáře nejsou vítány. P.S.: Osobně útočné a odborně velmi nekvalitní komentáře, zejména velmi dlouhé, budou mazány.