Génius jako Galileo si poradí i bez vyspělé techniky

Mnoho lidí si pod dojmem hollywoodských filmů představuje génia jako počítačového experta, který brilantně zvládá ty nejsložitější počítačové programy. Genialita se ale projevuje, i když génius nemá k dispozici prakticky nic.

Třeba fyzikálního génia si většina lidí představí jako tvůrce a řešitele šíleně složitých matematických rovnic například v obecné teorii relativity, kvantové mechanice nebo teorii super-strun, což je nejnadějnější teorie "všeho", která by měla popsat vše v našem vesmíru.

Jenže se na druhé straně zdá, že geniální skoky ve vědě odstartovává mnohdy nová, nicméně velice prostá myšlenka. Darwinova představa evoluce jako vývoje živého od jednoho prostého základu po nejsložitější a velmi rozmanité formy života je vlastně velmi jednoduchá. Stejně jednoduchá je i představa, že se čas skutečně zpomaluje a délky skutečně zkracují, která stála u zrodu Einsteinovy speciální teorie relativity. Jednoduchá je též představa, že gravitační přitažlivost je vlastně totéž jako když zrychlujeme nějaké těleso působením síly (princip ekvivalence), tento Einsteinův základ obecné teorie relativity.

Nádherný příklad takové jednoduché myšlenky předvedl Galileo Galilei při odvození představy setrvačnosti. Zákon setrvačnosti říká, v Newtonově formulaci: "Jestliže na těleso nepůsobí žádné vnější síly, pak těleso setrvává v klidu nebo v rovnoměrném přímočarém pohybu." A Galileo si jej dokázal odvodit úžasně jednoduchým způsobem vlastně z pádu tělesa v gravitačním poli.

Tradované klišé, že Galileo studoval volný pád těles házením předmětů z věže na Náměstí  svatého Marka v Benátkách nebo ze Šikmé věže v italském městě Pise, se zdá být pouze výmyslem. Nebo to přinejmenším není tím hlavním, co ho přivedlo k představě, že všechna tělesa padají v tíhovém poli Země se stejným zrychlením. U lehkých předmětů by totiž jeho pozorování znehodnotil odpor vzduchu. Každý asi pochopí, že papírová koule bude padat kvůli odporu vzduchu pomaleji než stejně velká železná koule.

Asi i proto Galileo zvolil raději pouštění kuliček po nakloněné rovině. Na té totiž kuličky dosahují podstatně menších rychlostí a tím je odpor vzduchu prakticky zanedbatelný. Navíc v té době neexistovaly hodiny, které by uměly měřit vteřiny a části vteřin, takže Galileo používal jako hodiny vlastní počítání/odhad času. Měl tedy značně omezenou přesnost měření času, která by nebyla dostatečná při volném pádu (té jeho části, kdy je odpor vzduchu nepodstatný), což si zřejmě vynutilo nakloněnou rovinu. Toto řešení bylo navíc praktičtější, neboť se vešlo do "laboratoře". A taky kdo by chtěl tahat pořád nějaké těžké koule na věž? :-)

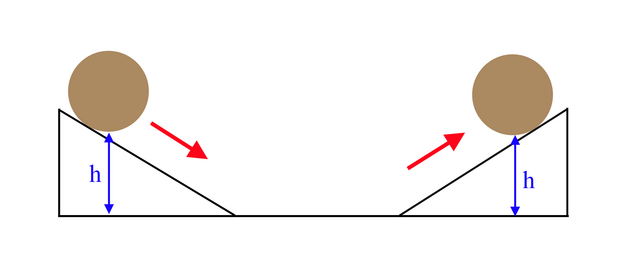
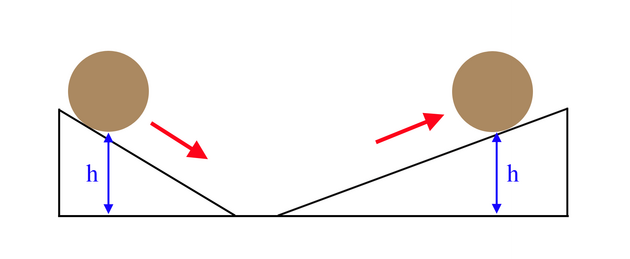
Galileo při svých pokusech s nakloněnými rovinami zjistil, že když spustí nějakou kuličku z výšky h po nakloněné rovině, vystoupá na protější stejně nakloněné rovině opět do výšky h (viz obrázek výše). Pak ale také zjistil, že i když má druhá nakloněná rovina jiný sklon, opět kulička vystoupá do přesně stejné výšky h (tření a tím i ztráty energie byly vzhledem k přesnosti jeho měření zanedbatelné). Viz obrázek níže.

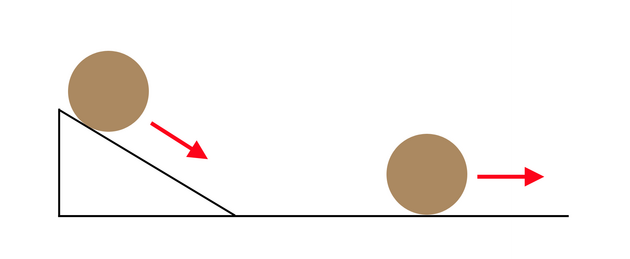
Tím vlastně formuloval zákon zachování energie při její přeměně z gravitační potenciální energie do pohybové a zpět. Na začátku ve výšce h je koule v klidu, pak se začne pohybovat a když vystoupá na druhé nakloněné rovině do výšky h, na chvilku se zase zastaví, než se začne vracet zpět. A pak se Galileo geniálně zeptal, kdy se kulička zastaví, když protější rovina bude nakloněná méně a méně, až nebude nakloněná vůbec a bude tedy vodorovná, viz následující obrázek.

Pochopil, že se tato koule nezastaví nikdy a bude se pohybovat věčně (pakliže si odmyslíme třetí). Takovou extrémně prostou, dle mého geniální úvahou došel k principu setrvačnosti. Úžasný nápad!

Ale aby to nevypadalo, že odmítáme high-tech nebo složité výpočty (což pochopitelně není pravda), připomeňme si, jakou high-tech Galileo použil. Měl to štěstí, že byl v jeho době vynalezen dalekohled. Dalekohled byl opravdu náhodně objeven v Holandsku, Galileo nebyl jeho objevitelem. On jej jen dokázal zdokonalit natolik, že jako první vyrobil na tu dobu špičkový dalekohled, který výrazně opticky významně přibližoval vzdálené objekty. Galileo měl štěstí i v tom, že žil v té době v Benátkách, a tak měl nedaleko ostrov Buráno, kde se rozvinulo skvělé sklářství. Proto si zvládl pořídit špičkový 8x zvětšující dalekohled. To byla na tu dobu světově špičková high-tech. Tento dalekohled vyrobil ale dost proto, že ho pak za dobré peníze mohl prodat benátskému dóžeti, jako vojenský pozorovací nástroj, který viděl nepřátelské lodě podstatně dříve než prosté oko.

Jenže už na tom je vidět, že si uměl dopředu představit dopad nově vznikajícího přístroje. A opět prostá myšlenka, že ho použije i k pozorování vesmírných těles z něj udělala absolutní vědeckou hvězdu. Zjistil totiž, že nebesa nejsou dokonalou hudbou sfér, jak se předpokládalo od Aristotela, ale třeba že jsou na Měsíci hory a údolí jako na Zemi, a že tedy Měsíc není žádná ideální koule. Spojil tak zdánlivě dokonalou nebeskou sféru s viditelně nedokonalými ději na Zemi.
(Chcete-li číst podobné blogy, přidejte si blog tohoto autora mezi oblíbené červeným tlačítkem "Přidat blogera k oblíbeným" na pravé straně.)