Jak vědci (ne)dokázali nekonečnost vesmíru
Teda byla to hra, dejte mi něco absolutního a já vám dokážu, že to nemůže existovat. Nekonečno (to pravé, ne potenciální) je totiž jen jeden z případů něčeho skutečně absolutního. Tuhle hru si chci dnes zahrát s pořadem BBC "Jak velký je vesmír" a předním kosmologem Seanem Carrollem.
V tomto pořadu se totiž uváděla následující úvaha, která byla označena jako důkaz nekonečnosti vesmíru: Ze školy dobře víme, že součet úhlů trojúhelníku je přesně 180 stupňů. To ale platí jen v rovině, která není deformovaná. Pakliže je onen trojúhelník třeba na povrchu Země, tedy na něčem zakřiveném, součet jeho úhlů už není 180 stupňů. Na obrázku níže je jasné, že zvolený trojúhelník (vyznačený červeně) musí mít součet úhlů větší než 180 stupňů, neboť oněch 180 stupňů dávají dohromady už dva úhly na rovníku. A k těmto 180 stupňům musíme připočíst ještě třetí úhel, úhel umístěný na Severním pólu.
Existují i mnohé jiné typy zakřivení, kde může být součet úhlů třeba i menší než oněch 180. Nám ale bude stačit fakt, že pouze u trojúhelníku v dokonale ploché (eukleidovské) rovině je součet úhlů přesně 180 stupňů.
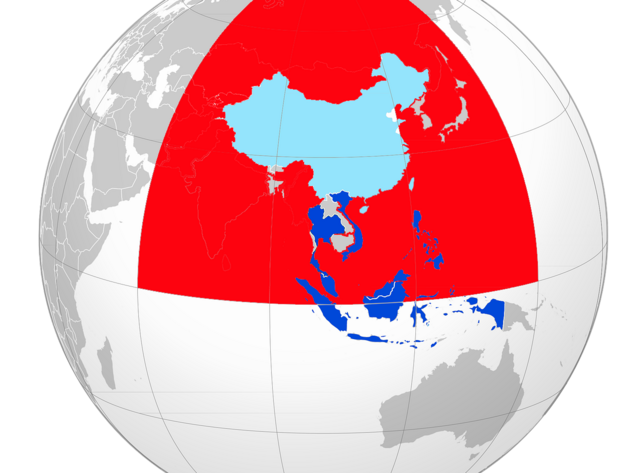
Úvaha uváděná v onom pořadu analyzovala trojúhelník, tvořený dvěma paprsky, které k nám letí ze vzdálenosti přes 13 miliard světelných let. Byly to dva paprsky reliktního záření, to jest záření, které vzniklo poměrně krátce po velkém třesku. Třetí stranu tvořilo místo lokálního zvýšení teploty tohoto záření, neboť jeho teplota není dokonale rovnoměrná. Na mapě níže jsou to červené oblasti. V této úžasně elegantní úvaze vzal Sean jako třetí stranu úsečku, která spojuje nejvzdálenější body jednoho takového červeného "fleku".
Sean uvádí, že s přesností na tři desetinná místa určil, že součet úhlů tohoto trojúhelníku je 180 stupňů. To ale znamená, že úhel může být 180,0005 nebo 179,9995 stupňů a nemusí být přesně 180. Ale i tak Sean dokázal, že je vesmír úžasně obrovský ve srovnání s tou částí o rozměrech 13,7 miliard světelných let, kterou vidíme.
Uvažme, že se na zhruba 14 miliardách světelných let může paprsek zakřivit jen o 0,0005 stupně. A aby byl vesmír (nad)koulí, podobně jako Země, musel by se paprsek vlastně otočit o 360 stupňů (v analogii obkroužit Zemi, nebo by musela čára na Zemi obtočit celou Zemi). Stačí tedy prostá trojčlenka, abychom odhadli nejmenší možnou velikost vesmíru podle tohoto měření:
Nejmenší možná velikost vesmíru = 13,7 miliard světelných let x 360 stupňů / 0,0005 stupně
Výsledek je 986 400 miliard světelných let, tedy vesmír je zřejmě nejméně 72 tisíckrát větší než to, co vidíme. Úžasný výsledek, ne? Úžasná představa. Ale na druhé straně, i kdyby byl vesmír miliardkrát větší než to, co vidíme, tedy měl rozměr 13 700 000 000 miliard světelných let, kolikrát je větší nekonečno? No přece nekonečněkrát.
Carrollův důkaz tedy není ani omylem důkazem nekonečnosti našeho vesmíru, dokonce je od tohoto důkazu nekonečně vzdálen. Můžeme si věc přiblížit tak, že abychom měli z podobného měření jistotu, že je vesmír skutečně nekonečný, museli bychom měřit absolutně přesně, neboli s přesností na nekonečně mnoho desetinných míst. Takové měření je ale absolutně nemožné, neboť každé měření má určitou chybu, která nemůže být nulová. Jiný příklad nedosažitelnosti nekonečna v praxi si můžete přečíst v článku Tajemné nekonečno jednoduše.
Všimněme si, že kdybychom chtěli dokázat nekonečnou velikost vesmíru, museli bychom už mít nekonečnou přesnost měření, tedy něco jiného nekonečného. Je to začarovaný kruh. Abychom dosáhli nějakého nekonečna, už bychom museli mít jiné nekonečno. A protože žádné zatím (v realitě) nemáme, nebudeme ho mít nikdy.
Tohle lze vzít jako axiom nenulové nepřesnosti každého měření, neboť jsme za dobu existence civilizace prováděli takové množství měření, že miliarda je v tomto množství nepatrná. A všechna tato měření vždy měla nenulovou nepřesnost. Ostatně Sean tím, že sdělil přesnost měření na 3 desetinná místa, přiznal možnou chybu o velikosti 0,0005 stupně.
Platí-li axiom nepřesnosti měření (axiom NM), pak z toho ale plyne, že nelze žádným měřením dokázat existenci nekonečnosti čehokoliv v realitě. Žádné měření, žádný praktický důkaz není absolutní, absolutně přesný a absolutně spolehlivý. To by pak ostatně nešel ani zobecnit či jinak zrelativizovat. Představa takového absolutního empirického důkazu je ale nevědecká, neboť takový důkaz by byl nefalzifikovatelný (v Popperově smyslu). Falzifikovatelnost je totiž nutnou podmínkou vědeckosti nejen důkazů, ale jakékoliv teorie, myšlenky či sdělení.
Tím jsme předvedli princip neexistence nekonečna (v realitě), tedy to, že (aktuální) nekonečno není vědecký pojem, ale jen pohádka vzniklá z "náboženského" vytržení plynoucího z neschopnosti lidstva nekonečno pochopit. Nekonečno (v realitě) je jen iracionální emoční představa. Tak prosté chyby v úvahách mohou dělat geniální vědci, když použijí místo racionální úvahy emoční nadšení. (Další rozbor neexistence nekonečna v realitě naleznete třeba v článku Proč je nekonečno pavěda.)
Ve zmíněném pořadu správně uvedli, že nekonečnost vesmíru je nejjednodušší řešení. To mi ale připomnělo aforismus: "Na každou složitou otázku existuje jednoduchá odpověď. Pochopitelně špatná." :-)
————————————————————————————————————
P.S.: V tomto blogu jsme se pro jednoduchost vyhnuli tomu, že ani v matematice neexistuje žádné aktuální nekonečno (např. ani množinu přirozených čísel nelze aktualizovat), jen nekonečna potenciální. Jestli ale někoho toto téma zajímá, může kouknout na článek Nekonečno jako mechanický bůh.
P.P.S.: Uviděli jsme, že pouze součet úhlů trojúhelníků v rovině může být přesně 180 stupňů. To je ale zjednodušení, neboť jestliže se křivost místo od místa mění, může být prostor i prapodivně zakřiven a stále může být součet přesně 180. Tato možnost je ale málo pravděpodobná. Otevírá to nicméně otázku, jestli opravdu mezi námi a oním místem reliktního záření o jiné teplotě, je prostor stále rovnoměrně rovný/křivý, když víme z obecné teorie relativity, že každá těleso prostoročas zakřivuje.
P.P.P.S.: Prapodivné také je, jak dokázal Sean změřit ty dva vzdálené úhly. Asi jen nepřímo ze změření toho úhlu blízkého a předpokladů, jak vypadají ty dva vzdálené. Nepouštěl jsem se ale do tohoto rozboru, neboť mým jediným cílem v tomto blogu bylo předvést, že nekonečno se dokázat nedá.
Jan Fikáček, Ph.D.
Fake news o historii vztahu Izrael-Palestina

To hlavní z historie oblasti najdete v minulém blogu, který překvapivě zařadila do „Zaujalo nás“ redakce blogů iDnes. Dnes uvedeme na pravou míru některé pomýlené pověsti o této oblasti a nahradíme je historickými fakty.
Jan Fikáček, Ph.D.
Proč jsou izraelská média daleko méně proizraelská než česká?

A nejde jen o izraelská média. USA jsou přece dlouholetý a věrný spojenec Izraele, ale ani ony nestojí teď vždy na straně Izraele. Proč? Proč se snaží válečné tažení Izraele brzdit a volají po příměří?
Jan Fikáček, Ph.D.
Tak přece má foton hmotnost!?

Fyzika je úžasná věda, která proměnila celou naši civilizaci. Stačí vzpomenout třeba jen elektřinu bez níž by nebyly počítače, mobily, TV, osvětlení našich bytů atd. Ovšem výjimečně se v ní objeví i dost iracionální tvrzení.
Jan Fikáček, Ph.D.
Solvay institut - Einstein, Schrödinger, Planck, Heisenberg, Bohr atd.

Od roku 1911 se konají Solvayovské konference, kterých se ve dvacátých letech účastnili dnes nejslavnější fyzici jako Einstein, Planck, Bohr, Heisenberg. Tyto konference jsou známé hromadnými fotografiemi nejslavnějších fyziků.
Jan Fikáček, Ph.D.
Nahraďte svou ženu a děti umělou trpělivostí (inteligencí?)!

Tak jo, uznávám, že ženu a děti nelze umělou inteligencí nahradit ve většině případů, ale v jednom by to asi šlo, ne? :)
| Další články autora |
Nahá umělkyně za zvuků techna házela před dětmi hlínou. Už to řeší policie
Policie prošetřuje vystoupení, ke kterému došlo na Akademii výtvarných umění (AVU). Umělkyně a...
Stovky amerických obrněnců se v řádu dnů nepozorovaně přemístily do Česka
Několik set vozidel americké armády včetně obrněnců Bradley nebo transportérů M113 se objevilo ve...
Přes Česko přešly bouřky s krupobitím. Dálnici D1 pokrylo bahno a větve
Do Česka přišly přívalové deště, na některých místech padaly i kroupy. Hasiči hlásili desítky...
Německo je otřeseno. Přišel brutální útok na politika, pak následoval další
Na lídra kandidátky německé sociální demokracie (SPD) v Sasku do evropských voleb Matthiase Eckeho...
Vyváděla strašné věci. Zahradil označil Jourovou za nejhorší z eurokomisařů
Premium Když Česko vstoupilo 1. května do Evropské unie, byl tam matador ODS Jan Zahradil kooptován...
Z uprchlíka agentem. Šapošnikov sehrál při výbuchu ve Vrběticích klíčovou roli
Premium Jakou roli hrál ve výbuchu muničního skladu ve Vrběticích bývalý ruský voják Nikolaj Šapošnikov? O...
Rusko bombarduje civilní cíle a chlubí se tím. Nechutné, říkají Ukrajinci
Premium Záporoží (od zpravodajů iDNES.cz) Areál stavební firmy v Záporoží nacházející se jen dva kilometry od centra města zasáhla raketa...
Severní Makedonie zvolila novou prezidentku. Předchůdce uznal porážku
Severomakedonský prezident Stevo Pendarovski uznal porážku ve středečním druhém kole prezidentských...
Izrael otevřel přechod Kerem Šalom, pomoc se k civilistům přesto nedostává
Do Pásma Gazy ve středu přes klíčové hraniční přechody na jihu oblasti nepřicházela žádná...

Jak předejít syndromu náhlého úmrtí kojence?
Syndrom náhlého úmrtí kojence (SIDS – sudden infant death syndrome) je doslova noční můrou všech rodičů. V současné době lze tomuto zbytečnému...
- Počet článků 311
- Celková karma 29,54
- Průměrná čtenost 3139x
Chcete-li sledovat diskuse v "jeho" skupině, připojte se do Vědecké filosofie & Fyziky (nejen). jfikacek@gmail.com
Upozornění: Toto je popularizační blog pro veřejnost, neberte ho tedy jako vědeckou dizertační práci. Někdy je to jen divoká fantazie. Na druhé straně se snaží udržovat jistou vědeckou kvalitu, takže "esoterické" komentáře nejsou vítány. P.S.: Osobně útočné a odborně velmi nekvalitní komentáře, zejména velmi dlouhé, budou mazány.